Firstly, it is worth differentiating quantum superposition from Heisenberg’s uncertainty principle- the former representing the non-classical simultaneous occupation of two (seemingly exclusive) states, and the latter being a constraint on the measurement of a system or state.
The most well known example of superposition is Schrodinger’s cat, but I think I can do one better. Firstly though, I’ll give a very brief overview of Heisenberg’s uncertainty principle.
Heisenberg’s uncertainty principle might be best used to describe the position/momentum of an electron around the nucleus of an atom. Much like the planets around the sun, they orbit the nucleus (with the addition of some other funkier shapes). However, rather than existing in a fully realised position like we might use to calculate the passing of a year as the earth orbits the sun, they exist in a probabilistic ‘cloud’; represented by a wave-function rather than being wholly particle-like.
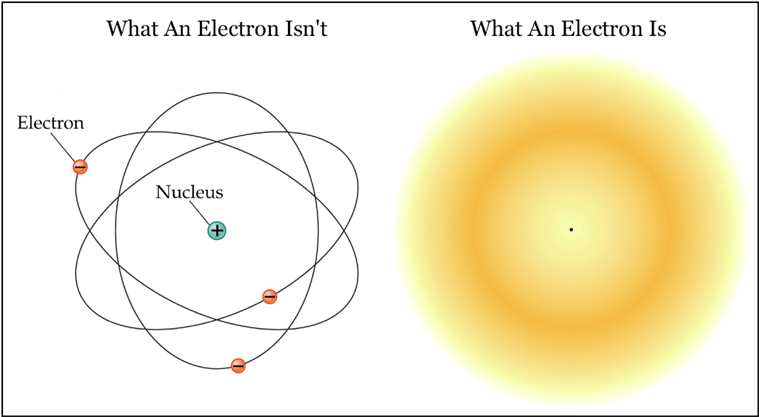
The ‘degrees of freedom’ of an electron (the variables and qualities that describe it) vary dependent on the system you are modelling, and how you choose to describe it. In a canonical ensemble in Statistical Mechanics for instance (looking at the statistical properties of large groups of particles), you might model it using Cartesian coordinates for position and momentum (x,y,z,px,py,pz), and spin states (up, down), whereas in the case of a single atom, you might instead describe it using polar coordinates and angular momentum instead, due to the spherical nature of the system and its behaviour. Without getting too lost in the details, essentially some of these qualities are ‘non-commutable’, meaning that the more certain you are of one of these properties, the less sure you are of the other. For example, we have position vs momentum, the uncertainty principle represented by:
Δx⋅Δp≥ℏ/2
Where Δx is the uncertainty in position, and Δp is the uncertainty in momentum. The product of these uncertainties must be at least as large as ℏ/2, where ℏ (the reduced Planck constant) is a universal quantum constant that sets the minimum scale at which quantum effects become significant. Essentially though, to reiterate, this equation means that the more we reduce the value of the uncertainty in x (knowing it’s position more confidently), the more the value of the uncertainty in p increases (and the less confident we are on it’s momentum) – and vice versa, as it is bound by the condition for the multiple of both to be at least the value of ℏ/2.
Without all of the semantic double negatives: As one value of uncertainty decreases, the other increases.
While this does represent the behaviour of the actual physical phenomena, mathematically this is an artefact of the method of analysis used – Fourier Transforms, and graphically/visually, in a loose-weave sense it amounts to whether we are looking at the wave-function in terms of a ‘spike’, or ‘spread’ (and which variable – x or p – we are analysing for).

On the left in red we have position (note that the wave-function 𝚿 is in terms of x), on the right in blue we have momentum. On the top we have a more uncertain momentum (spiked/clustered position, spread momentum), and on the bottom a more uncertain position (spread of position, spike/cluster of momentum). Essentially, for the upper left case, the position is bound to a smaller area – for the bottom left, it is more of a ‘spread’ of potential positions.
We could also look at the dimensional analysis of the equation, concentrating on the value of ℏ. ℏ, being given in units of Joule Seconds / Radians – relating the energy of a wave to it’s frequency, and another way of representing the uncertainty principle is:
ΔE⋅Δt≥ℏ/2
Showing the non-commutable relationship between Energy and Time, instead of Position-Momentum (remember- the way we choose to define the model of the system in our approach changes the ‘degrees of freedom’ or variables, and thus different qualities will emerge as non-commutable).
Remember, the fundamental nature of quantum systems is that they are probabilistic; statistical. When looking at large groups of particles we can usually analyse the overall behaviour of the group, but on an individual basis this is much more difficult. You can think of it in terms of the Galton Board:

The overall behaviour of the system is predictable and repeatable; however if you were to attempt to predict where an individual marble will end up, you’d find it a lot more difficult. This is why on a classical level Newtonian dynamics suffices for the purpose of predicting physical systems, but not so well in the sub-atomic and quantum domains.
So how can a particle exist as a purely probabilistic entity? Does that mean it’s random? I’m glad you asked.
I like to think of it in terms of paradox, and I’m going to constrain it to the degree of freedom of ‘spin states’ for the purposes of this example, however it can also apply to spatial position, energy levels, and other qualities.
Firstly though, I’m going to give an intuitive linguistic example. Imagine the following sentence:
This sentence is false.
Lets say we approach it with the assumption that it is initially true, (it works approaching it the other way too, though), reading it slowly. Assuming it is true, then it follows that once we have read it the whole way through and digested its total sentiment, then it must be false. However there is a cyclical nature to its overall sentiment, reading it again – being self-negating, as its falsehood now must be false, meaning that it is true. Lets imagine that we continue this recursive process, but begin reading it faster and faster, until the oscillation between True and False seem to blur and merge, and it’s truth value exists as both True and False simultaneously. Now, if we were to press the figurative stop button on this process, at any one point, our discernment of whether it is true or false would collapse into one or the other (as we are no longer reading it ‘infinitely fast’, we settle on one or the other), but the process by which this is decided would be entirely random.
This is the linguistic equivalent of the superposition of spin states in a closed time-like curve (CTC) interpretation, whereby the oscillation between two symmetrically opposite states happens within the bounds of an ‘instantaneous’ repeating cycle. Imagine the following:
The Earth orbits around the Sun, returning to the same position (relative to the frame) once per year. Now imagine that it moves so fast that it returns to the same position within a day. Now, so fast that it catches up to itself at the moment it leaves- creating an unbroken line where it exists all around the orbital path at the same time.
Now, we look at another interesting property of spinning matter in nature, the oscillation of poles. The magnetic field of the earth is said to flip approximately every 250,000 years or so due to the geomagnetic dynamo (spinning magma in its core), having a relatively slow spin. When we look at something faster however, the behaviour emerges more obviously:

Now imagine this much much faster and on a much smaller scale- so that it behaves like our CTC. It would exist not in one direction, but in both simultaneously until stopped, or ‘observed’; a superposition of spin states.
Essentially, this is potentially what is happening on the quantum scale, with electrons occupying multiple states in superposition, being, in their nature, spinning/oscillating energy at a very fast frequency.
The nature of superposition then, is essentially a physical manifestation of a paradox with some funky time mechanics mixed in.
When we ask the question “Does god play dice with the universe?”, the answer is: rolling enough dice, there are predictable patterns. But each die individually is yet undetermined. And remember- it’s not one total roll; life and time are continuous processes, and one small change in a variable at one time can plausibly affect the conditions and results of the next – just as the butterfly causes a storm, the result of one die can cause radical changes later on down the line.
If we do have free will, it comes by way of a synergy between mind and quantum processes, a mechanism of ‘orchestrating’ quantum states (see Orchestrated Objective Reduction), by which decisions can exist in superposition – pushed this way or that in a synergistic relationship with consciousness.

Leave a comment