Most of us have heard of the famous cat in the box- both dead and alive; a thought experiment intended to highlight the unintuitive behaviour of physics at a quantum level. Well, a cat being dead and alive is a very strange and unintuitive way of describing it as far as I’m concerned- and there’s a better way to explain it (I love you Schrodinger – no hate).
Superposition is a physical example of paradox. Paradoxes being not unnatural, but an inherent behaviour of reality. However they usually take a moment for people to get their mind around, as they require an ‘outside the box’ approach instead of being ‘in’ the system- otherwise they’ll send you dizzy with the alternations. But what are the parts that make up this physical paradox? With the linguistic paradox we had a sentence and a truth value… To my mind: This quantum paradox or ‘superposition of states’ is a photon spinning along a closed time-like curve in a microscopic imaginary circular spatial dimension with a degree of freedom expressed in a mobius-like (or ‘spinor’) twist. A closed time-like twistor-spinor.
Great. Now what the fuck does that mean?
The Earth we know orbits and rotates around the sun, returning to the same space (relative to the inertial frame – the solar system itself is moving around the quasar at the center of the galaxy). There are many such examples of circular repetition we can conjure to mind. However, imagine that instead of just returning to the same position in space, something returns to the same position in space-time. How does that look?
Imagine a man deciding to go for a walk in a circle, lets say a few meters in radius. This man represents a photon travelling in a circular dimension. Light in a circle – “but it only travels in straight lines!”, I hear you say. The space itself is curved and circular, and so from the position of the light- it is travelling in a straight line, but relative to outside observers it appears to curve. This can be thought of as an extreme example of ‘gravitational lensing’ as observed on the cosmic scale – however in this example, is due to the circular nature of space at small scales (I will go into more detail on this). Light is also pretty fast, so as he walks around, he speeds up.
As this light-man speeds up, he gets so fast that he begins to catch up to himself, and can soon see the back of his own head. As he speeds up just a little more, he catches up to himself completely, and exists at all points along the circular path- having arrived at the point in space and time where he started from. He is a circular blur.
Now we add a ‘degree of freedom’ in the form of the man with either his thumb up or thumb down. He can choose when along his journey to switch between the two, but for the sake of this example lets assume he changes it every time he goes round once completely – he spends half of his time with his thumb up, and half of his time thumb down. Now, in addition to this closed time-like ‘blur’ of spatial superposition: when stopped by an observer passing by- he exists in either thumb up or thumb down, but before being observed- he existed in both states simultaneously.
In reality, this spin superposition is likely more due to the direction of the spinning- is it clockwise or counterclockwise; the observer just sees a blur until they stop him and find out which way he’s going. Generalising to 3 dimensions, the circular path he walks on can also rotate ‘up and over’ as if spun on an axis also- further changing the direction of the spin. The direction of this spin also often doesn’t have any bearing on direction in ‘real space’ that we observe, but only in the bubble of the CTC (imagine a ball-bearing free to spin in a liquid – that is how the pocket dimensions behave- free to rotate within the rest of space). The exception of this being magnetic particles such as in iron bar magnets- this is best illustrated with a drawing, and the geometry of these pocket dimensions accurately describes the observed magnetic fields lines. We have to remember that the photon isn’t simply a particle or a line, but a sinusoidal propagation of electro-magnetic waves; the way those waves interact with each other within the inner bounds of the CTC, and the way they manifest and behave ‘outside’ of the circular path are of particular interest (and maybe the reason for stablizing ‘centripetal’ forces), but perhaps beyond this post for now.
Anyway; we’ve got a pretty good conceptual framework for the superposition of spin states using CTCs and a circular space-time. But what about that magical ‘entanglement’ we’ve heard so much about?
Entanglement can be said to be a symmetry expressed in spin states- ‘magically’ when an entangled pair of electrons are separated by a distance, observing the spin state of one automatically implies the state of the other being opposite- instantaneously, regardless of the distance. This ‘faster than light’ transfer of information is notable because usually the speed of information is bounded by the speed of light- light is the fastest information carrier in the universe, and nothing can travel faster. Einstein called quantum entanglement ‘spooky action at a distance’. So what’s going on here?
Essentially quantum entanglement can be thought of as a wormhole between two halves of the same particle. The formal theory of this is known as ‘ER=EPR’, and makes the equivalence of entanglement (Einstein-Podolsky-Rosen; EPR) and an Einstein-Rosen bridge (or wormhole), i.e. ER.
Information doesn’t have to travel faster than the speed of light if two objects separated by a great distance in ‘real space’ occupy the same point in another space- in fact, it follows intuitively that they would act at the same time, being two halves of the same thing.
Let’s go back to the example of the walking man. We will use the thumb up and thumb down example to illustrate the point first, and then maybe generalise to the direction of rotation afterwards.
The man, walking along this circular path, notices that the circle has become a giant mirror, and whichever direction his thumb points he inevitably finds that his reflection’s thumb is pointing the other way relative to himself. Him being in a superposition, his thumb is both up and down, as is that of his reflection. However- when he is stopped, and the superposition collapses into a defined state, it follows that the spin state of his reflection must be the opposite. This reflecting mirror would be better described as a portal to another point in ‘real space’, with the two halves of the system existing ‘entangled’ and symbiotically in this CTC frame, but disparate and separate in real space. It is also worth noting that the characteristic behaviours of a wormhole that are needed in order for it to be stable is a ‘rotation of the throat’, that is to say- the wormhole ‘tube’ must be spinning in order that it doesn’t collapse on itself- something that intuitively follows from this way of thinking about it; if we wish to visualise the two particles in ‘real space’ instead of our CTC space, we split the frame along the line of the symmetry and extend both sides away from one-another until we have a spinning cylinder – both ends representing a different point in ‘real space’. (I’ll do some sketches for this at some point – and show it in terms of the direction of rotation instead of the thumb pointing also).
Where do these circular dimensions come from, then? Why do we see space and time as linear at all observable scales, but apparently not at the smallest? I admit that the ‘reason’ for this is less of an explanatory ‘why’, and more of a few different ways of thinking about it. After all- ‘why’ is space linear otherwise..? It just is.
Anyway, for those of you familiar with the golden spiral- we often start from the center and build out, but I’d like to do the opposite to make my point; we see this curved line approaching from the outer bounds of infinity- each of these boxes representing a difference in scale. The curved line traces from corner to corner of each square, but what of that of the first and smallest square? Does it go corner to corner? I think it twists in on itself, into the plane of the page. That is to say, in real three dimensional space, these extra circular dimensions exist at a ‘right angle’ to real space. There, but not on the plane we observe from.
Furthermore- with this first square of the golden ratio, the only requirement for the dimensions of the first square is that they are the same magnitude as the second in order to fit on the page. For those familiar with imaginary numbers, we know that i*i = -1, something again initially unintuitive, as the square of any number shouldn’t result in a negative. However, we often find imaginary numbers in the fundemental equations used to describe quantum systems. But if we take the imaginary number and define the lengths of the sides of this first square as i and -i, when we calculate the area, we are given 1, the same as the next square- and the fibbonacci sequence can continue on it’s merry way. The first two squares while functionally identical in this frame, are fundementally different in their makeup.
If we’d like to visualise this a little better- we need look no further than the shape of a gastropod shell. (I will include this image in the former versions as I think it’s particularly important).
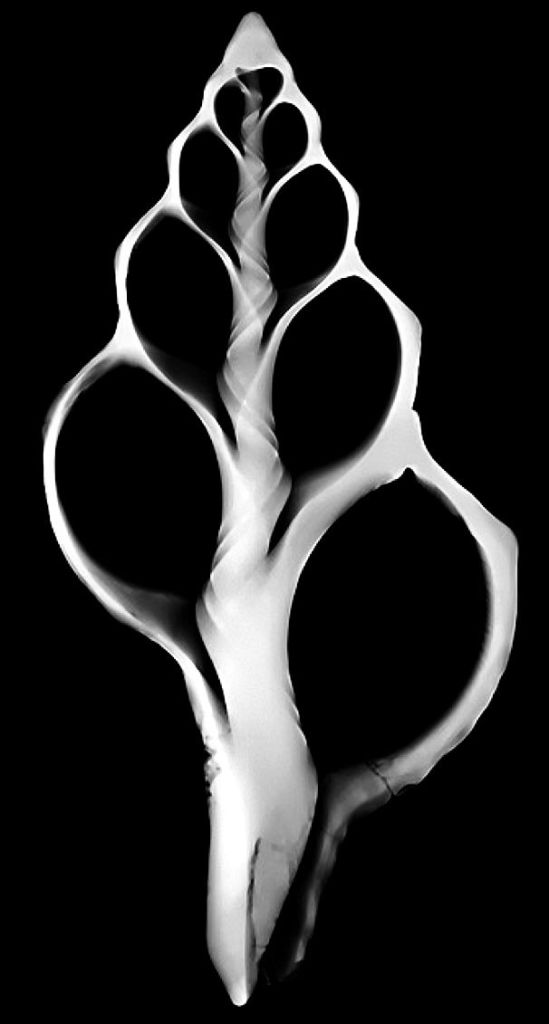
If we look at this shell ‘face on’ then we see a spiral tending to a point. However, it is at this point that (given a cross-section), we can see the rich inner twist that moves through the center of the shell. This is how I imagine the spinning photon compared to real space, in some sense. A photon halted in its tracks in real space, forced to act out it’s constant speed of light in a space at right angles to real space, appearing to spin in place.
This golden spiral then, or the golden ratio- is observed in nature across scales, and the spiral phenomena everywhere. It is a fundemental geometry of nature. I’d also hazard an educated guess that the distribution or ‘density’ of primes correlates somewhat accordingly to that of the golden spiral, and it might be this imaginary component that causes a deviation from a ‘normal’ and ‘real’ progression of primes. Anyway, at the smallest scales, there is a spatial equivalence of the smallest ‘real space’ and the quantum ‘imaginary space’ that behaves differently. The real space is linear, and the imaginary space is ‘twisted in’ on itself, as in the first square of the golden spiral or the center of the gastropod shell. Rather than something that ‘just makes the maths work’ in quantum systems, the imaginary number represents a physical quality of reality. An imaginary dimension.
When we see the imaginary number ‘i’ often sat nicely next to hbar (reduced Planck’s constant) in Schrodinger’s equations – is it not clue enough? The smallest meaningful measure of space (Planck’s constant), divided by 2*pi (the circumference of a circle), multiplied by the imaginary number. Schrodinger didn’t conjure this equation from nothing; what we have here is an imaginary circle at the smallest scales, already used to describe quantum systems. I don’t mean to ‘reinvent the quantum wheel’, but I feel it’s pertinent to remind people what this all means, visualise it effectively, and from this level of understanding we can begin to extrapolate and explain other meaningful phenomena- at the quantum scale and otherwise.
What I would state then- in a conclusive paragraph, is that all things in the universe are some formation of light; matter simply being spinning light tied to a local frame, much like our earth is tied to the sun. I will delve more into what this means in terms of the forces of nature (including quantum gravity), hadrons, and neutrinos in the next post- and we will build up to dark matter, dark energy, and the arrow of time in due.. course?

Leave a comment